논문 작성을 위해 통계 공부하는 초보자입니다. 전문가에게 맡겨서 한다는 분들도 많은데, 왠지 직접 공부해보고 싶어 져서 시작해 봅니다. 그런데 처음부터 난관이 많네요. 대학교 다닐 때 한 과목 통계학 개론을 들었던 것 같은데 잊어버린 지 오래고, 새롭게 시작하려니 용어도 익숙치 않고, 어찌 되었든 여러 논문을 공부하려니 알아야 하는 통계 용어들이 많아서 하나씩 하나씩 정리해보고자 합니다.
상관관계 (Correlation, 相關關係)
상관관계는 두대상이 서로 관련성이 있다고 추측되는 관계를 의미한다고 합니다. A와 B과 관련이 있다라고 논리적으로 이야기하고 싶을 때 주로 자주 사용하는 단어입니다.
"A와 B는 상관관계가 있다"
그런데 어느정도 상관관계가 있는지에 대해서 알아야 하는 경우가 있습니다.
단순히 A와 B가 100이라는 관계 중에 1개의 관계가 있는 건지, 100의 관계가 있는 건지 아니면 (-) 마이너스 음수의 관계가 있는 건지 등을 파악해야 하는 경우가 있습니다. 이러한 경우 나타나는 값을 상관계수(correlation coefficient)라고 합니다.
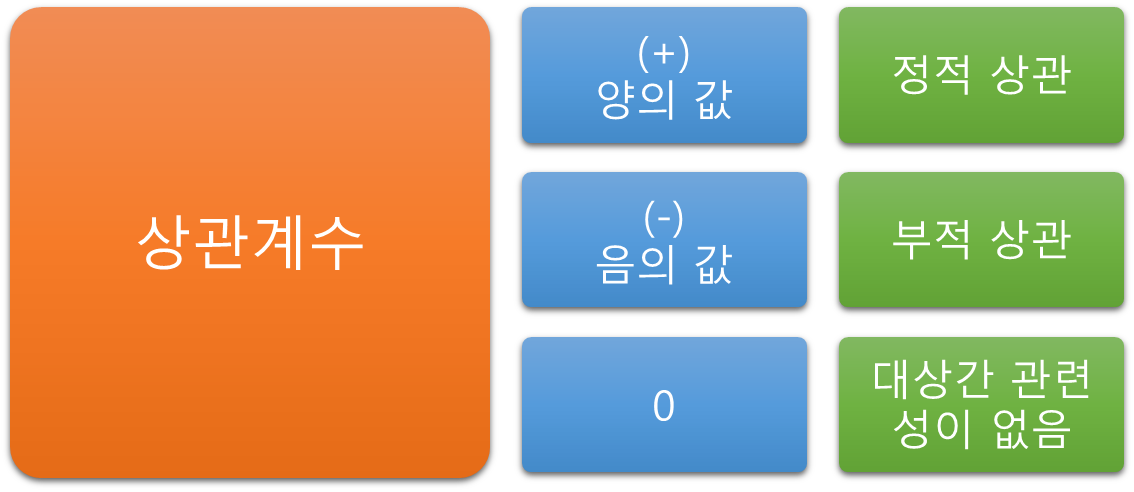
이러한 계수 값이
양의 값 즉 (+)값을 가질 때 정적 상관이 있다고 이야기하고, 음의 값 (-) 값을 가질 때 부적 상관이 있다고 이야기합니다. 다시 아이기하면 양의 값이든 음의 값이든 계수가 나오면 A와 B는 상관이 있다고 이야기할 수 있는 것입니다. 만약 (+) 0.8의 값을 갖는다면 0.8만큼의 정적 상관이 있다고 이야기하고, (-)0.7의 값을 갖는 다면 -0.7만큼의 부적 상관성이 있다고 이야기합니다.
즉 상관계수는 양의 값이든 음의 값이든 부호에 상관없이 숫자의 절대값이 클수록 관련성이 크다고 해석합니다.
그러면 논문에서 보이는 상관관계 통계표는 어떻게 해석하나요?
다음의 표를 예로 들어 보면

이 표는 각각의 요인 (채택여부, 사업특성....등등)간의 상관계수를 나타나낸 상관관계 표입니다. 조금 다르게 표현하기는 표의 형태도 있지만 대체적으로 위와 같은 형태를 취하고 있습니다.
이 표를 보면 일반적으로 두 변수간의 관계를 알 수 있는데, 먼저 이익집단과 전문성의 상관관계가 0.733으로 높게 나타나있는 것을 볼 수 있다. 이경우 정적 상관관계가 크다라고 이야기 할 수 있고,
경제성장률과 실업률과의 관계를 살펴보면 -0.824의 값을 가지는 것으로 부적 상관 관계가 크다라고 이야기할 수 있습니다.
상관계수의 해석시 유의해야 할 점
상관계수가 0.5 이하인 경우는 두 변수 간의 선형적인 관계가 약하다는 의미를 갖고 있습니다. 일반적으로 상관계수의 절댓값이 0.8 이상이면 강한 상관관계, 0.6 이상이면 상관관계, 0.4 이상이면 약한 상관관계, 0.4 이하이면 거의 상관관계가 없다고 말합니다.
그래서 상관계수가 0.5 이하인 경우는 두 변수가 함께 변하는 정도가 낮다고 해석할 수 있습니다.
예를 들어, 한 학생의 수학 점수와 영어 점수의 상관계수가 0.3이라면, 수학 점수가 높은 학생이 영어 점수도 높을 가능성이 약간 있지만, 확실하지는 않다고 볼 수 있습니다. 반대로, 수학 점수가 낮은 학생이 영어 점수도 낮을 가능성이 약간 있지만, 확실하지는 않다고 볼 수 있습니다. 즉, 두 과목의 성적은 서로 크게 영향을 주고받지 않는다고 할 수 있습니다
그렇지만 상관계수가 0.5 이하인 경우에도 두 변수가 인과관계를 가질 수는 있습니다.
예를 들어, 담배를 피는 횟수와 폐암 발생률의 상관계수가 0.4라면, 담배를 피우는 횟수가 많을수록 폐암 발생률이 높아지는 경향이 있지만, 담배를 피우는 것이 폐암의 유일한 원인은 아니라는 것을 의미합니다. 즉, 상관계수가 0.5 이하인 경우에도 두 변수 사이에 다른 요인들이 영향을 미칠 수 있으므로, 단순히 상관관계만으로 인과관계를 결론 내리는 것은 위험할 수 있습니다.
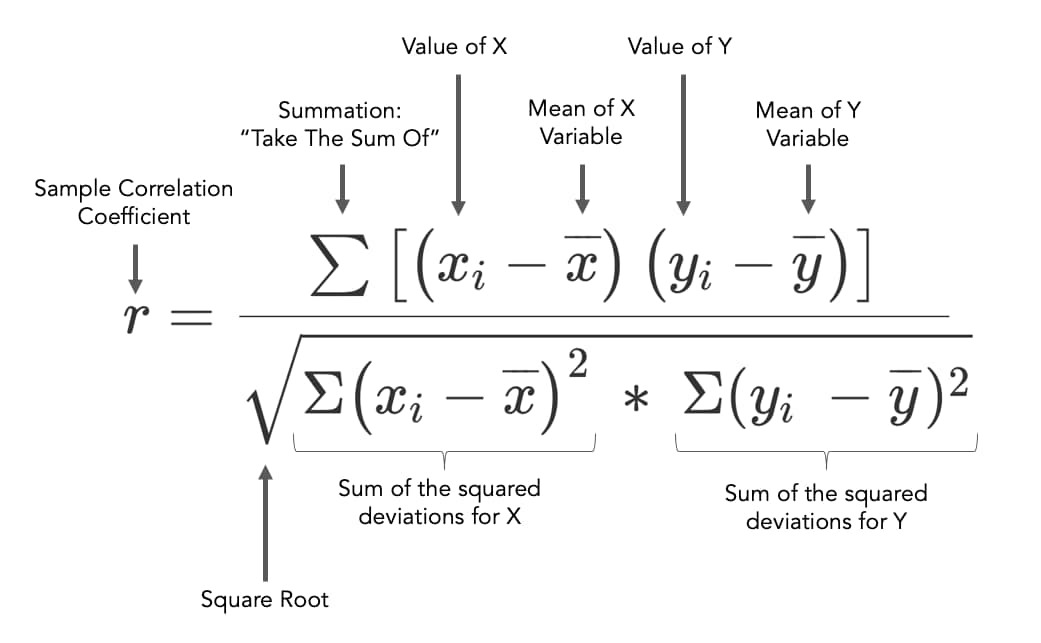
상관계수의 계산
상관계수는 두 변수의 선형적인 관계의 강도와 방향을 나타내는 척도로, 공분산을 표준화한 값으로 나타냅니다, 공분산은 단위에 영향을 받지만, 상관계수는 단위에 영향을 받지 않습니다.
상관계수를 계산하는 방법은 여러 가지가 있습니다. 가장 기본적인 방법은 피어슨 상관계수를 구하는 공식을 사용하는 것입니다.

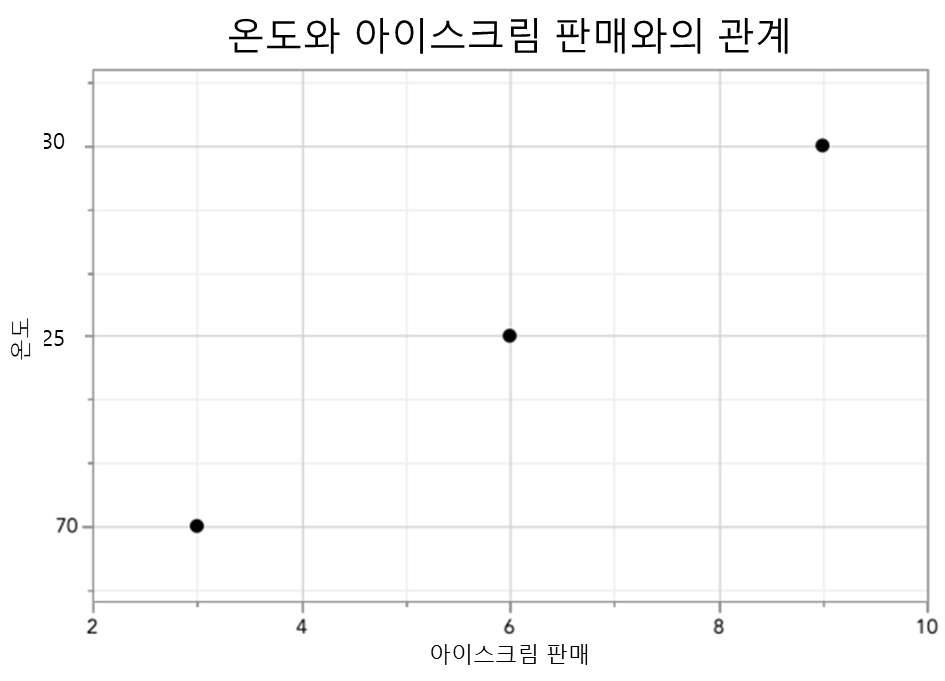
온도와 아이스크림 판매량의 상관관계를 예를 들어 보면
| 아이스크림 판매(x) | 온도(y) |
| 3 | 20 |
| 6 | 25 |
| 9 | 30 |
1. 상관관계를 분석하기 위해서 먼저 평균을 구하는 것에서 시작합니다.
표본의 평균은 아이스크림 판매 $\bar{x},와 온도 \bar{y}$ 기호로 표시하며, 다음과 같이 계산합니다.
$\bar{x}=\left\{ 3+6+9\right\}=6$
$\bar{y}=\left\{\left\{20+25+30\right\}/3 \right\}=25$
2. 평균을 구했으면 각각의 데이터들이 평균에서 얼마나 떨어져 있는지를 계산합니다.(거리 계산)
| 아이스크림판매(X) | 온도(Y) | ||
| 3 | 20 | 3 - 6 = -3 | 20 - 25 = -5 |
| 6 | 25 | 6 - 6 = 0 | 25 - 25 = 0 |
| 9 | 30 | 9 - 6 = 3 | 30 - 25 = 5 |
이제 상관계수 계산의 다음 부분을 계산합니다.
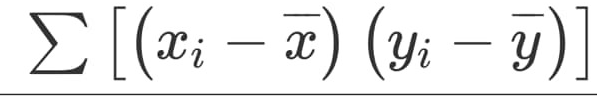
[ (-3)×(-5)] + [(0) × (0)]+[(3) × (5)] = 30
이제 분모 부분을 계산합니다.
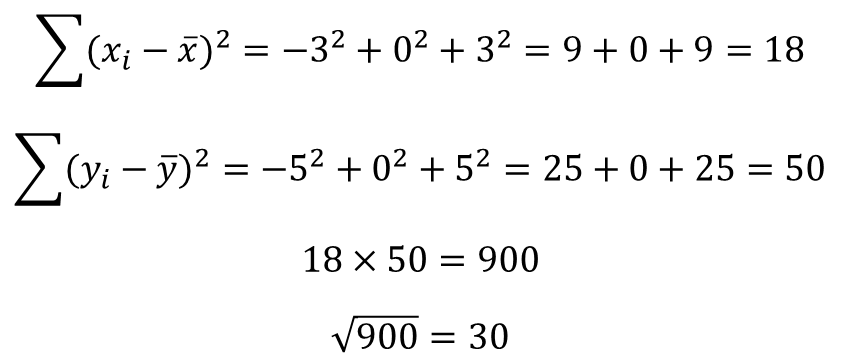
이제 상관관계 계산을 진행합니다.
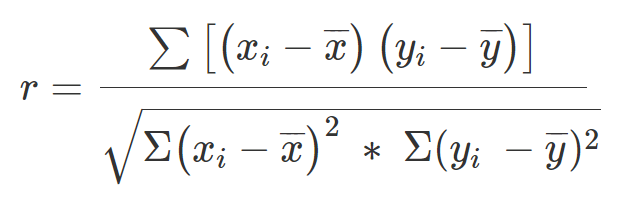
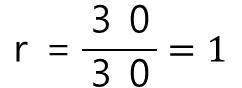
이해를 돕기위해 단순한 데이터를 예시로 제시했습니다.
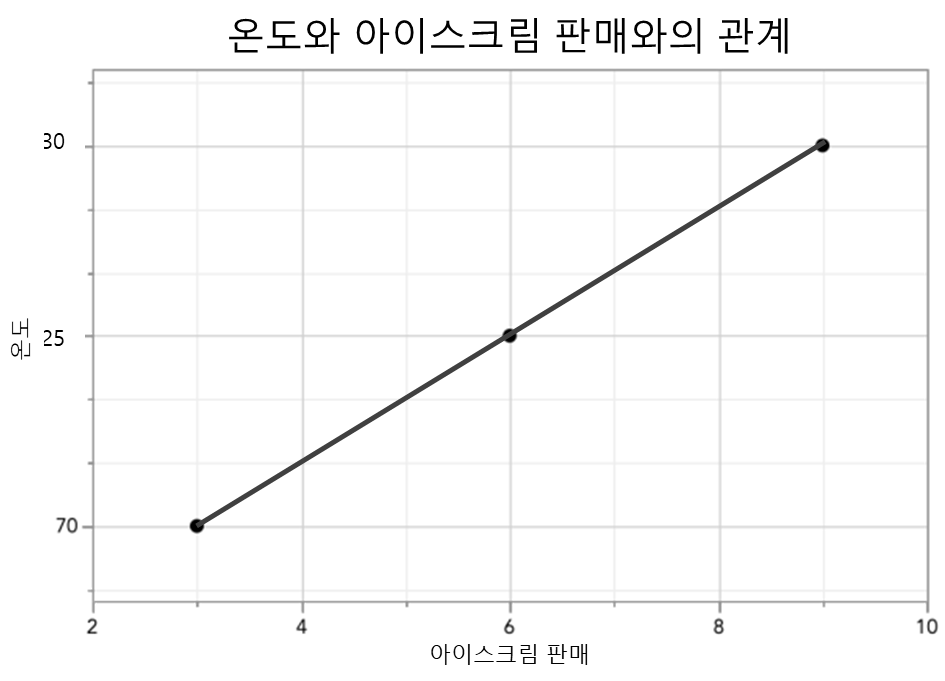
산점도를 나타내는 것은 가설 검정에 유용한 도구입니다.
그렇지만 상관계수가 0 이거나 0에 가깝다고 해서 변수 간의 관계가 없는 것은 아니며, 단순히 선형관계가 없다는 것을 의미한다는 것을 유의해야 합니다.
상관계수 중 pearson 상관계수(r)의 경우, -1에서 1사이에서 움직이며, 상관계수의 부호는 두 변수의 관계의 방향(direction)을 나타냅니다. 상관계수와 공분산의 부호는 일치하므로, 이와 같은 해석은 앞선 공분산과 일치한다. 그리고 상관계수 r의 절대적 크기는 관계의 강도(mgnitude)를 나타내게 되며, r의 절대값이 1에 가까우면 두 변수가 강력한 상관이 있다고 표현하고, 만약 r이 0에 가까운 값을 갖는다면 두 변수는 서로 상관이 없다는 것을 의미합니다.
엑셀로 구현하는 상관관계분석
이 방법은 엑셀에서도 쉽게 구현할 수 있습니다. 엑셀에서는 CORREL 함수를 사용하여 두 변수 간의 상관계수를 바로 계산할 수 있습니다. 예를 들어, A열과 B열에 각각 와 의 데이터가 있다면, 다음과 같이 입력하면 상관계수를 구할 수 있습니다
=CORREL(A:A,B:B)
엑셀에서 상관계수를 구하는 방법은 두 가지가 있습니다. 하나는 CORREL 함수를 사용하는 것이고, 다른 하나는 데이터 분석 기능을 사용하는 것입니다.
CORREL 함수는 두 변수의 상관계수를 바로 계산해 주는 함수입니다.
=CORREL(첫 번째 변수 범위, 두 번째 변수 범위) 형태로 입력하면 됩니다.
예를 들어, A열과 B열에 각각 x와 y의 데이터가 있다면, =CORREL(A:A, B:B)를 입력하면 상관계수를 구할 수 있습니다.
아이스크림 판매와 온도와의 상관계수를 구하고자 할 때 다음과 같은 데이터가 있다면
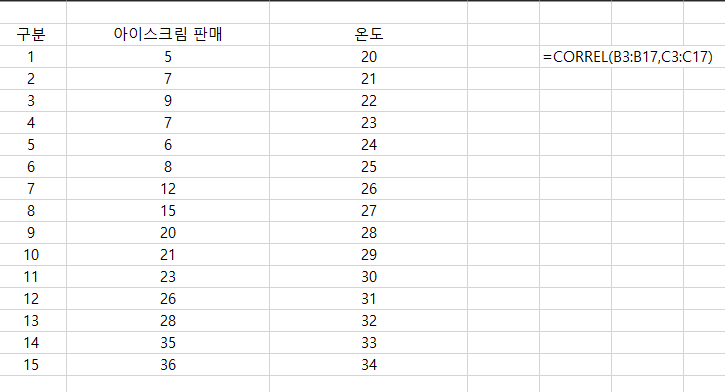
상관계수 계산하면 0.961773이 나왔습니다. 1에 가까운 수치로 매우 강한 정적 상관관계가 있다고 할 수 있습니다.
'논문, 통계학 공부' 카테고리의 다른 글
| 통계초보자의 인과관계 이해하기 2부 - 회귀분석, 이중차분법, 도구변수법 (3) | 2023.12.13 |
|---|---|
| 통계 초보자의 인과관계 이해하기 (2) | 2023.12.13 |
| 신뢰수준, 유의수준, 유의확률 (1) | 2023.10.29 |
| 모집단(population)과 표본(Sample) 그리고 표본 추출(sampling) (3) | 2023.10.28 |
| 논문과 변수 유형 (3) | 2023.10.28 |